Abstract

A crucial role for the success of the Artificial Neural Networks (ANN) processing scheme has been played by the feed-forward propagation of signals. The input patterns undergo a series of stacked parametrized transformations, which foster deep feature extraction and an increasing representational power. Each artificial neural network layer aggregates information from its incoming connections, projects it to another space, and immediately propagates it to the next layer.

Since its introduction in the ’80s, BackPropagation (BP) is considered to be the de facto algorithm for training neural nets. The weights associated to the connections between the network layers are updated due to the backward pass, that is a straightforward derivation of the chain rule for the computation of the derivatives in a composition of functions. This computation requires to store all the intermediate values of the process. Moreover, it implies the use of non-local information, since the activity of one neuron has the ability to affect all the subsequent units up to the last output layer.

However, learning in the human brain can be considered a continuous, life-long and gradual process in which neuron activations fire, leveraging local information, both in space, e.g neighboring neurons, and time, e.g. previous states.

Following this principle, this thesis is inspired by the ideas of decoupling the computational scheme, behind the standard processing of ANNs, in order to decompose its overall structure into local components. Such local parts are put into communication leveraging the unifying notion of constraint. In particular, a set of additional variables are added to the learning problem, in order to store the information on the status of the constrained neural units. Therefore, it is possible to describe the computations performed by the network itself guiding the evolution of these auxiliary variables via constraints. This choice allows us to setup an optimization procedure that is ``local’’, i.e., it does not require (1) to query the whole network, (2) to accomplish the diffusion of the information, or (3) to bufferize data streamed over time in order to be able to compute gradients. The thesis investigates three different learning settings that are instances of the aforementioned scheme: (1) constraints among layers in feed-forward neural networks, (2) constraints among the states of neighboring nodes in Graph Neural Networks, and (3) constraints among predictions over time.

Material

Download the slides here

Download the thesis here

Research questions and contributions

Constraint-based Neural Networks

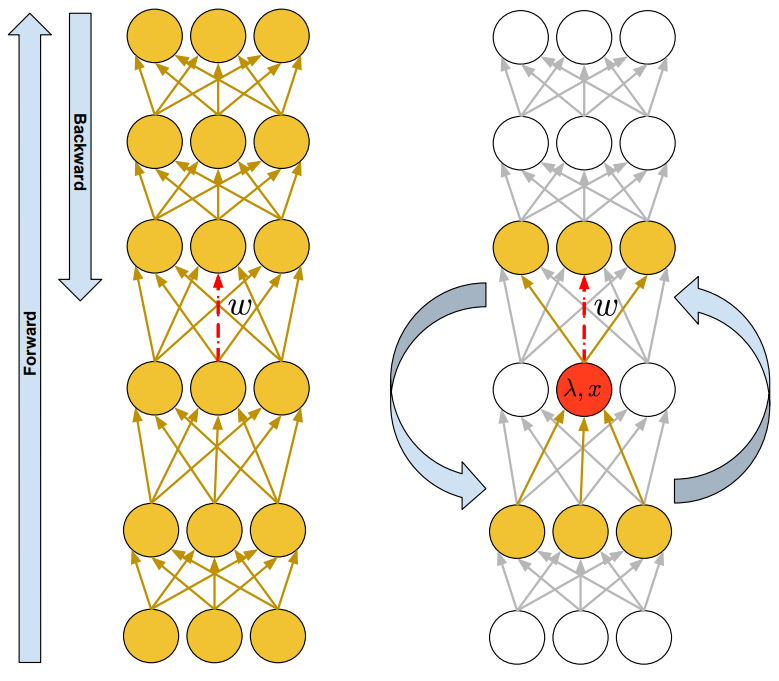BackPropagation has become the de-facto algorithm for training neural networks. Despite its success, the sequential nature of the performed computation hinders parallelizations capabilities and causes a high memory consumption. Is it possible to devise a novel computational method for a generic Directed Acyclic Graph that gets inspiration and advantages from principles of locality?

In the proposed approach, Local Propagation, DAGs can be decomposed into local components. The processing scheme of neural architecture is enriched with auxiliary variables corresponding to the neural units, and therefore can be regarded as a set of constraints that correspond with the neural equations. Constraints enforce and encode the message passing scheme among neural units, and in particular the consistency between the input and the output variables by means of the corresponding weights of the synaptic connections. The proposed scheme leverages completely local update rules, revealing the opportunity to parallelize the computation.

Based on “Local Propagation in Constraint-based Neural Network”, In International Joint Conference on Neural Networks(IJCNN2020)

Constraining the Information Diffusion in Graph Neural Networks

The seminal Graph Neural Networks (Scarselli et al., 2005) model uses an iterative convergence mechanism to compute the fixed-point of the state transition function, in order to allow the information diffusion among long-range neighborhoods of a graph. Is it possible to avoid such costly procedure maintaining these powerful aggregation capabilities?

The original GNN model encode the state of the nodes of the graph by means of an iterative diffusion procedure that, during the learning stage, must be computed at every epoch, until the fixed point of a learnable state transition function is reached, propagating the information among the neighbouring nodes. Lagrangian Propagation GNNs decompose this costly operation, proposing a novel approach to learning in GNNs, based on constrained optimization in the Lagrangian framework. Learning both the transition function and the node states is the outcome of a joint process, in which the state convergence procedure is implicitly expressed by a constraint satisfaction mechanism, avoiding iterative epoch-wise procedures and the network unfolding.

Based on “A Lagrangian Approach to Information Propagation in Graph Neural Networks”, In European Conference of Artificial Intelligence (ECAI2020)

and on “Deep Constraint-based Propagation in Graph Neural Networks”, In IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI)

Constraint-based Mutual Information Computation in Salient Areas of Video Streams

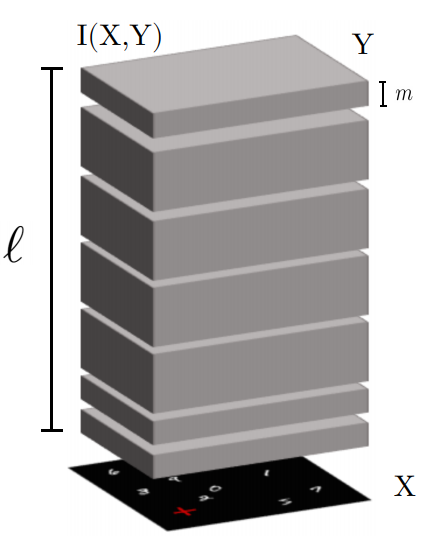Unsupervised learning from continuous visual streams is a challenging problem that cannot be naturally and efficiently managed in the classic batch-mode setting of computation. Lifelong learning suffers from the problem of catastrophic forgetting. Hence, the task of transferring visual information in a truly online setting is hard. Is it possible to overcome this issue by devising a local temporal method that forces consistency among predictions over time?

We consider the problem of transferring information from an input visual stream to the output space of a neural architecture that performs pixel-wise predictions. This problem consists in maximizing the Mutual Information (MI) index. Most approaches of learning commonly assume uniform probability density of the input. Actually, devising an appropriate spatio-temporal distribution of the visual data can foster the information transfer. In the proposed approach, a human-like focus of attention model takes care of filtering the spatial component of the visual information, restricting the analysis on the salient areas. On the other side, various temporal locality criteria can be explored. In particular, the analysis sweeps over the probability estimates obtained in subsequent time instants. Global changes in the entropy of the output space are approximated by introducing a specific constraint. The probability predictions obtained at each time instant can once more be regarded as local components, that are put into relation by soft-constraints enforcing a temporal estimate not limited to the current frame.

Based on “Focus of Attention Improves Information Transfer in Visual Features”, In Advances in Neural Information Processing Systems (NeurIPS2020)